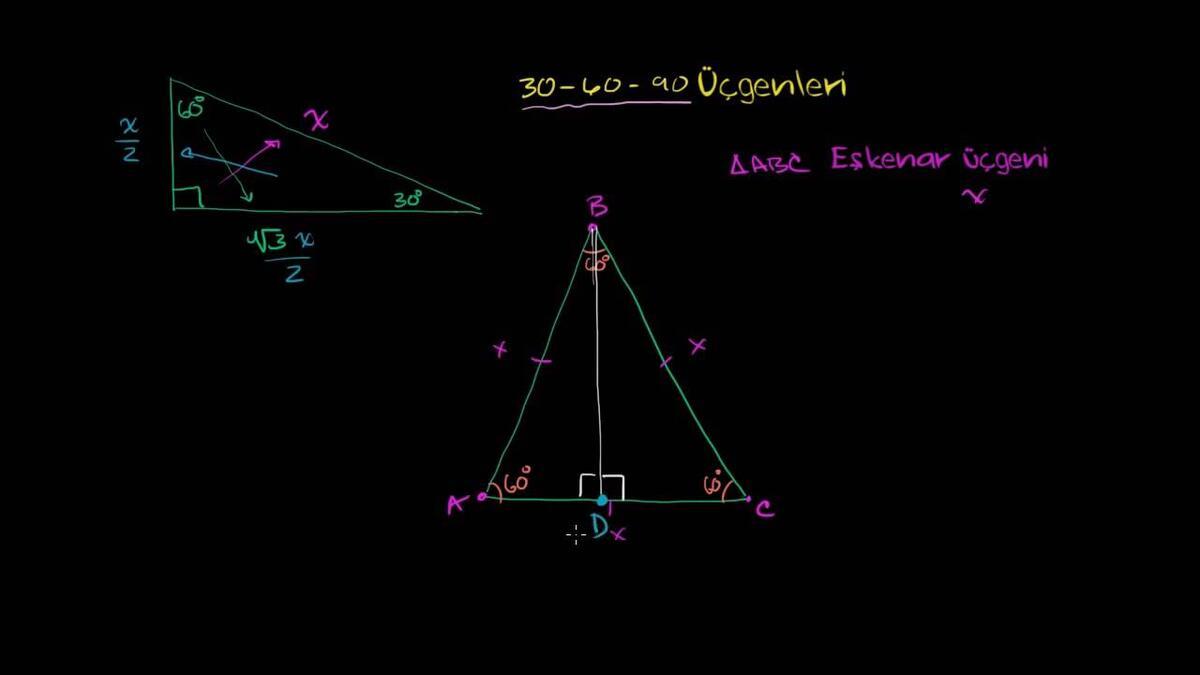
17 Ocak 12 16 Ocak 12 xMaTeMaTiK 0 yorum (15° 75° 90°) Üçgeni, (3 4 5) Üçgeni, (30° 30° 1°) Üçgeni, (30° – 60° – 90°) Üçgeni, (5 12 13) Üçgeni, İkizkenar dik üçgen, İKİZKENAR ÜÇGENI, ÖKLİT BAĞINTILAR, Üçgenlerde Uzunluk 30 60 90 üçgeninin özel üçgenler arasında yer almasının asıl nedeni iç açıları birbirine eşit olan ve her biri 60° olan ABC eşkenar üçgeninden 2 adet dik üçgen elde edilmesidirABC eşkenar üçgeni A açısından çizilen yükseklikle ikiye bölünür ve H noktası ile belirlenir Böylece ABH ve ACH isimli 30 60 90 üçgeni elde edilir 30 60 90 üçgeni olarak geçen bu kural hakkında öğrenciler kafasında birçok soru bulunmaktadır 30 60 90 üçgeninin kuralı nedir, özellikleri nelerdir gibi sorular öğrencilerin merak

Ispat 30 60 90 Ucgeninde Kenarlarla Acilar Arasindaki Iliski Tyt Geometri Ozel Ucgenler Youtube
90 60 30 üçgeni
90 60 30 üçgeni-"bu kesin 30 60 90 ucgenidir" * denir ama buyuk yanlistir zira 15 75 90 veya 225 675 90 ucgenleri olmasi da siddetle muhtemeldirAslında burada bir çift " üçgeni" ile bu soruyu çözebiliriz ABE üçgeninde 30 ve 90 derece duruyor, burada o zaman bu karşıdaki açı da 60 derece olmalı Yani buradaki AEB açısı da 60 olmalı BCD üçgeninde de 30 derecemiz var, 90 derecemiz var 180'e tamamlamak için burası 60 derece olmalı Ve işte ilk üçgenimiz Ve bu da ikinci üçgeni BED




Index Of Wp Content Uploads 17 10
30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan bisiklet zinciri tamamen işlevini yitirdiği gibi geometri de öyledir Üçgeni Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittir Bir dik üçgende dar açılardan birinin ölçüsü 15 derece ise, hipotenüs uzunluğu hipotenüse ait yüksekliğin 4Read özel üçgenler (30°60°90° üçgeni) from the story Matematik Formülleri by TheMuhammedALI with 2,101 reads wattys15, formüller, geometri Resime bakın
Kenarortay, hem yükseklik hem de açıortaydır Açıortay, hemüçgeni özellikle üçgen içerisindeki hem açı hem de kenarı bulma konusunda büyük kolaylık sağlar Aynı zamanda özellikle herhangi bir geometrik şekil doğrusunda, ortaya çıkarılan üçgeni üzerinden alan kolayca bulunabilir Aynı zamanda analitik geometri üzerinde de birçok farklı işlem yapma imkanı 30 60 90 üçgeni özel üçgenler içerisinde belki karşımıza en çok çıkan üçgendir Bir öğrenci neyi çok iyi bilirsem sırtım yere gelmez diye sorarsa bunun cevabı da sanırım 30 60 90 üçgeni olacaktır Çünkü geometrinin temelini üçgenler oluşturmaktadır Üçgenlerde de uzunluk, alan ve açı hesaplamalarında 30 60 90 üçgeninden çokça faydalanırız Bu üçgeni
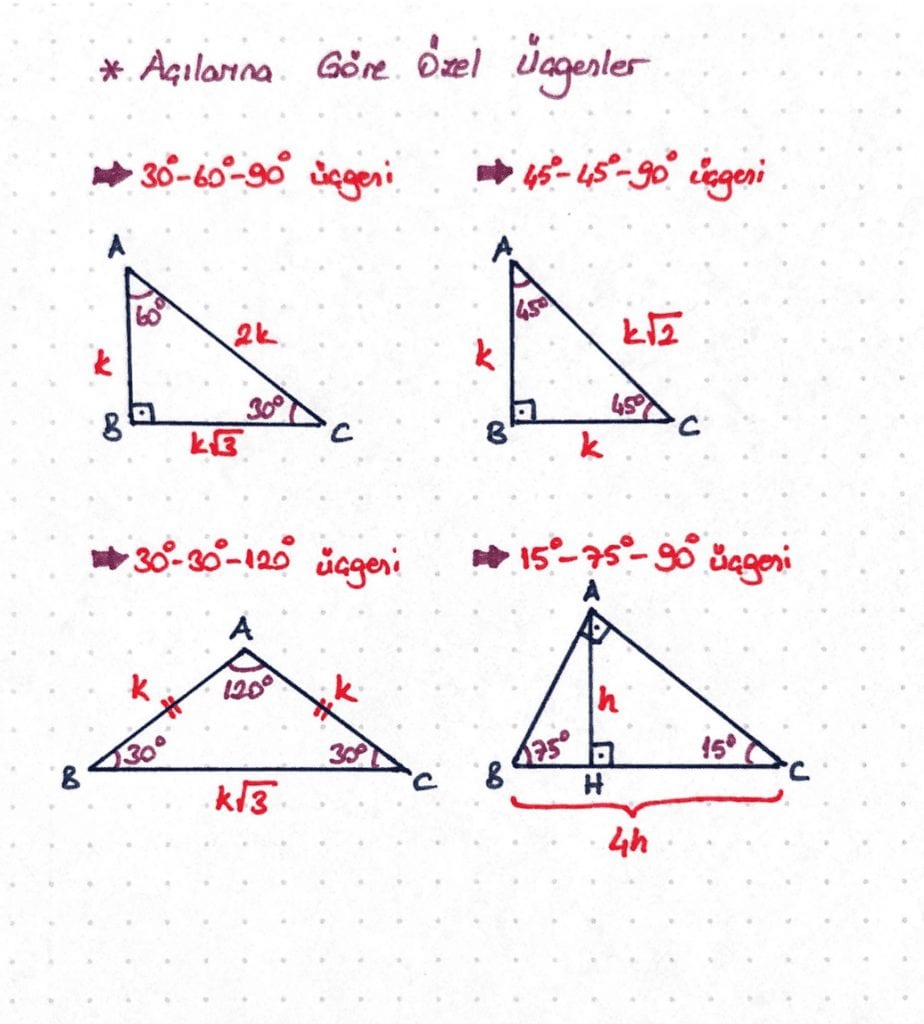
Üçgeni Kenar uzunlukları veya katları şeklinde olan dik üçgenlerdir AÇILARINA GÖRE ÖZEL DİK ÜÇGENLER Üçgeni Üçgeni 0 Üçgeni Üçgeni İKİZKENAR ÜÇGEN İkizkenar üçgende tepe açısından inen;Geometri konusundaki Üçgeni Kenar Oranları İspatı başlıklı ders videosuna buradan ulaşabilirsiniz Khan Academy TürkçeGeometri konusundaki Üçgeni ile İlgili Soru başlıklı ders videosuna buradan ulaşabilirsiniz Khan Academy Türkçe



Ozel Ucgenler Konu Anlatimi



1
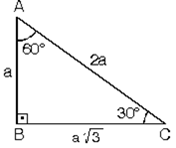
(30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° – 60° – 90°) üçgenleri elde edilir AB = AC = a BH = HC = pisagordan (30° – 60° – 90°) dik üçgeninde; 45 45 90 üçgeni de işimizi kolaylaştıracak özel üçgenlerden biridir 45 45 90 üçgenini iyi öğrenirsek temel bazı trigonometrik bağıntıları da öğrenmiş oluruz Bu nedenle bu üçgeni ve özelliklerini bilmek önemlidir Öncelikle en az bu üçgen kadar önemli 30 60 90 üçgeni olduğunu belirtelim Bu özel üçgenleProfessöre 60 BD Çiz Eşkenar Sonrası sende 1 votes Thanks 1 Yorumlar 90 60 30 üçgeni olur o halde A) 60 B) 90 C) ise 30 olur 0 votes Thanks 0 More Questions From This User See All Captainwarz April 0 Replies Answer Captainwarz March 0 Replies Answer Captainwarz March 0 Replies Answer Captainwarz March 0 Replies Answer
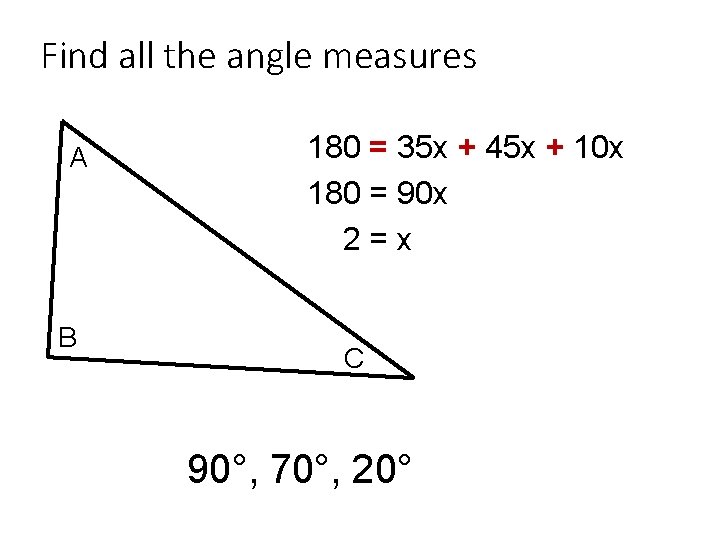



Triangle Sum Properties Objective Classify Triangles And Find
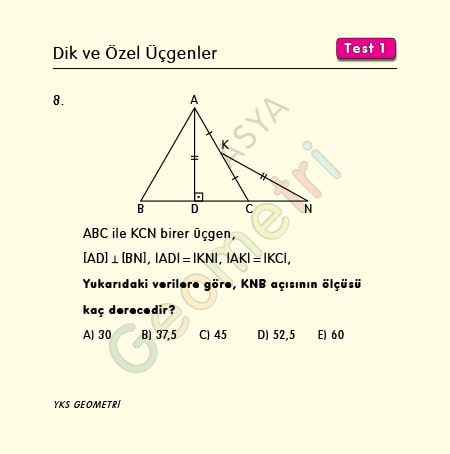



Vertical And Special Triangles Test 1
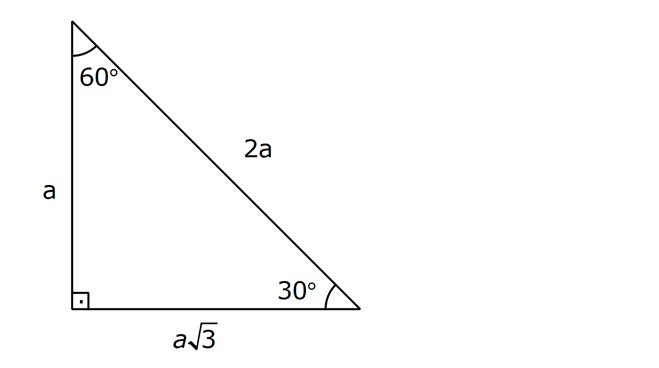
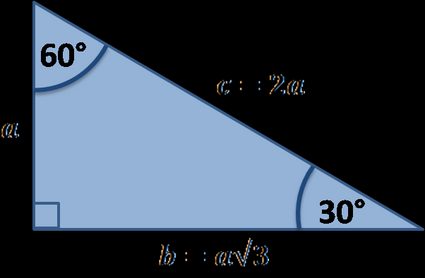
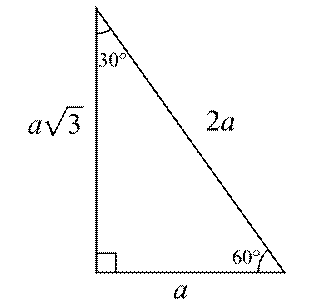
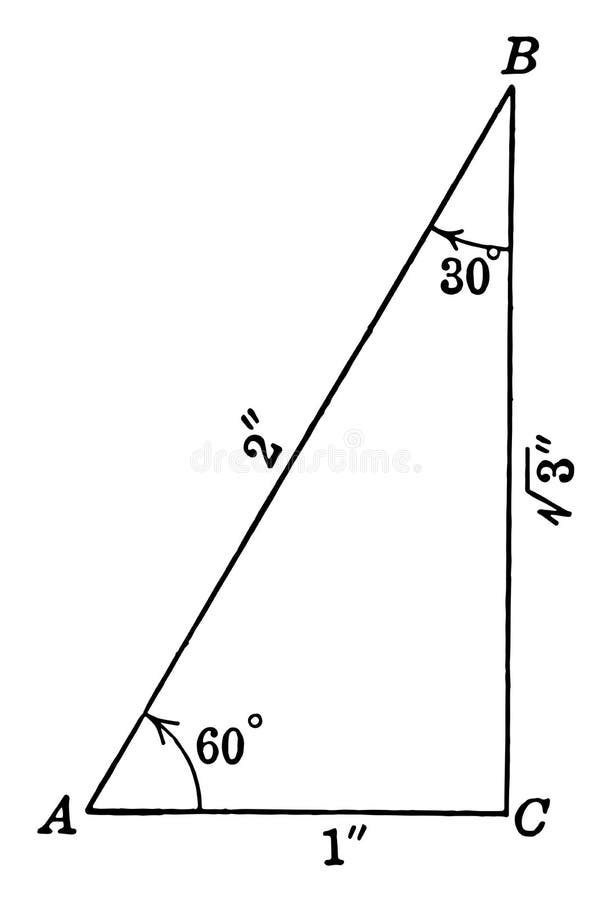
üçgeni içerisinde açılara bakmak suretiyle kenar uzunluklarının hesaplaması kolayca yapılabilmektedir Bu doğrultuda 30 derecenin karşısındaki kenar a olursa, 60 derecenin karşısındaki kenar ise a kök 3 olarak ifade edilir 90 derecenin karşısındaki kenar ise 2a olarak öne çıkar İşlem üzerinden dik üçgende herhangi bir kenar verildiği vakit, diğer#trigonometri #cos #costeoremi # #11sınıf #11matematik #trigo1Sen Anlat Hocam kanalı , mevcut bulunan derslerimizde sizlere yardımcı olabilmek için elİŞletmestkproje ÜÇgenİ 90 60 30 ÜÇgenİ gİbİ bİr baĞintisi var )




30 60 90 Ucgeni Basit Bir Soru Yapabilirsiniz Eodev Com




Answered A Abc Bir Dik Ucgen Ab 1 Bartleby
ABE üçgeninde 30 ve 90 derece duruyor, burada o zaman bu karşıdaki açı da 60 derece olmalı Yani buradaki AEB açısı da 60 olmalı BCD üçgeninde de 30 derecemiz var, 90 derecemiz var 180'e tamamlamak için burası 60 derece olmalı Ve işte ilk üçgenimiz Ve bu da ikinci üçgeni üçgeni özellikle üçgen içerisindeki hem açı hem de kenarı bulma konusunda büyük basitlık sağlar Aynı zamanda özellikle herhangi bir geometrik şekil doğrusunda, ortaya çıkarılan üçgeni üzerinden alan basitçe bulunabilir Aynı zamanda analitik geometri üzerinde de birçok ayrımlı işlem yapma imkanı sağlayan bir yapıya sahiptir Sabit kenarı veUcgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com 15 75 90 üçgenin kuralı 15 75 90 üçgenin kuralıEski sevgiliyi unutmak 3;4 24 x 6 cm bu 4 luruz 53 The 27 63 90 Triangle Robertlovespi Net



Brebeuf Org
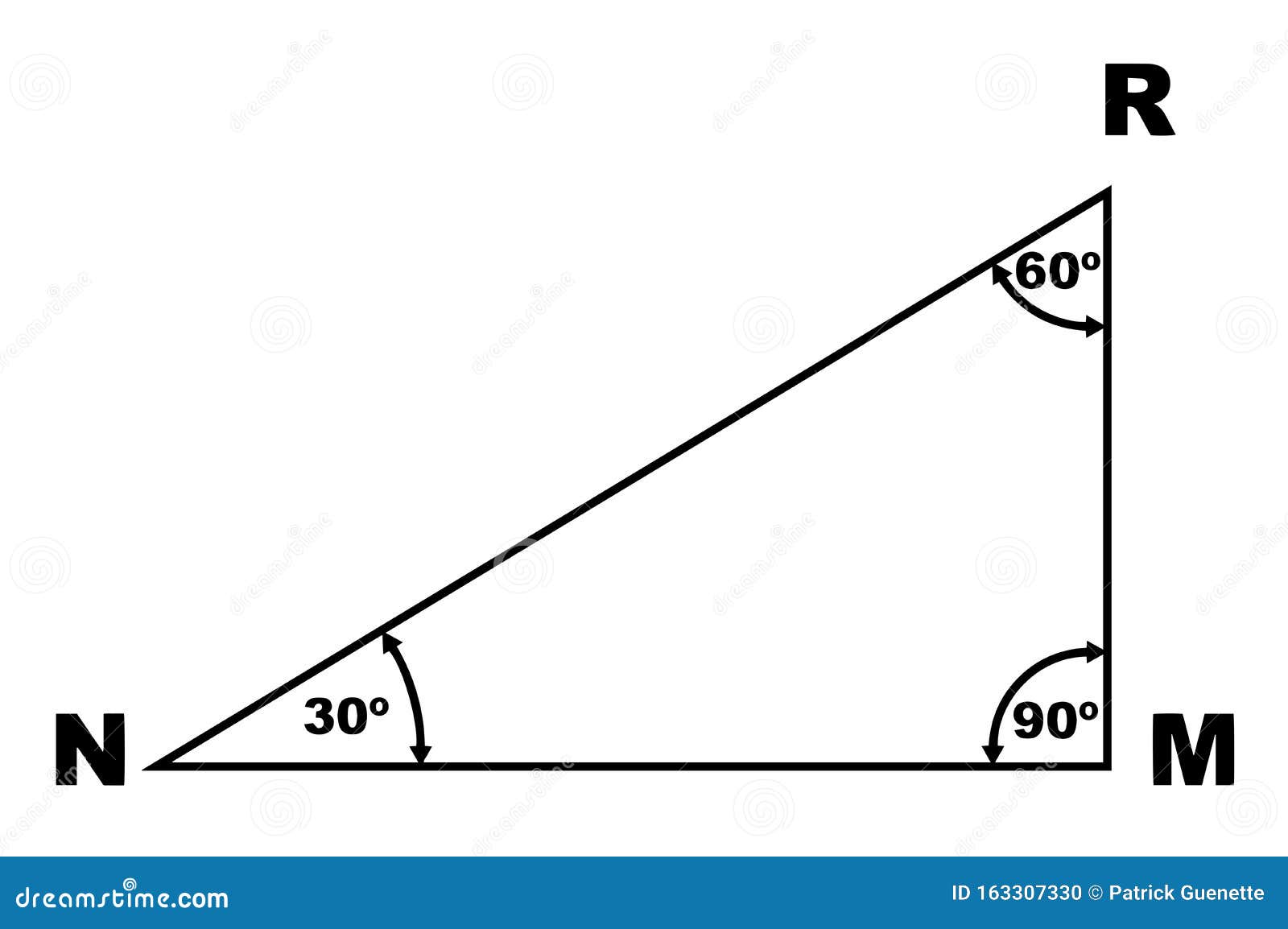



Triangle Degrees Stock Illustrations 251 Triangle Degrees Stock Illustrations Vectors Clipart Dreamstime
Büyük üçgen 30 60 90 üçgeni olur 90 'nin karşısında 6 2 var sa 30 nin karşısında yarısı olur 6 2 3 2 dir 2 45 45 90 üçgeninde 45 nin karşısında 3 2 var sa; 30 60 90 üçgeni matematiği ezberlenecek birşey sananlar için alemin en kral dik üçgenidir bir geometri sorusu cozumu sirasinda tikanildiginda akla gelen ilk ucgen turudur, diklik varsa soru bitmistir; 30°'nin karşısındaki kenarhipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö 3 katıdır(30° – 60° – 90°) dik üçgeninde;Hipotenüsü verilen derece dik üçgeni çizme » Search for Son Yorumlar Tam sayılı kesri bileşik kesre çevirme için Melis;
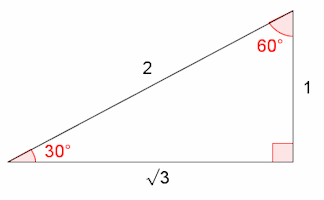



Common Trigonometric Ratios




Trigonometry Act Math
30 60 90 üçgeni kenarlarıBF, FG ve GB BFG üçgeninin kenarları olduğundan BF = FG = GB Sevgiler üçgenine yabancı biri için bu üçgen anlamsızdır ama tek bir çizgiyle biri ikizkenar diğeri bir üçgeni olan iki anlamlı üçgen elde ediverir Mühim olan az önceki soruda 45 ve 15 açılarında olduğu gibi bu açıları birbirinden30 – 60 – 90 ÜÇGENİ Eşkenar üçgendeA) 5 B) 6 C) 8 D) 10 E) 12 Çözüm m(ACB) 30 ise m(ABH) 180 90 30 60 dir Açıortaydan dolayı m(DBH) 60 / 2 30 dir BDH üçgeni bir 30 60 90 üçgenidir 30'un karşısı 2 3 ise, 60'ın karşısı 2 3 3 6 cm ABH üçgeni de 30 60 90 üçgenidir 30′ un karşısı 6 ise, 90'ın karşısı 12'dir Cevap 12 3490 nin karşısında 2 katı olur x 3 2 2 32 6 bulunur 32 wwwmatematikkolaynet AB BC AC CD m BAC 45 m CAD 30 BC 3 2 cm Yukarıdaki verilere göre, AD x kaç cm dir?




En Hizli 30 60 90 Ucgeni Ozellikleri



Math Figure 30 60 90 Triangle
0以上 15 75 90 üçgeni özelliği 75 90 özel üçgeni özellikleri 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan bisiklet zinciri tamamen işlevini yitirdiği gibi geometri de öyledir(30 60 90) Üçgeni (30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz




If Tan Theta 21 Show That Cosec 2 Theta Sec



Nanopdf Com
15 75 90 ÜÇGENİ KURALI NEDİR?Merhaba arkadaşım 😊Ben Matematik Kebapçısı 😊 Bu videoda senin için Geometride en çok kullanılan kurallardan üçgeninde açı ve kenar oranlarını anla 無料ダウンロード 15 75 90 üçgeni kuralı 75 90 üçgeni kuralı nedir Özel Ders Tadında Komple GEOMETRİ ( 36 nite 284 Video ) Sınavlara Hazırlık, Orta Öğretim, Lise, YKS, TYT, AYT, ALES,KPSS Puan 4,3 / 5 4,3 (4 puan) 61 öğrenci Oluşturan Öğrenci&Öğretmen Özel Ders Tadında Konu Anlatım Videoları Son güncelleme tarihi 12/ Türkçeüçgeni 22,5 derecenin




Ozel Dik Ucgenler Tekrar Makale Khan Academy



45 45 90 Ucgeni Matematikce
A) 4 3 B) 7 C) 5 3 D) 9 E) 10Kpss ile ilgili son gelişmelerden haberdar olun Kpss 19 Ders Dağılımları Mesleki Gelişim15 75 90 üçgeni Matematiğin geometri dalının özel formülü olan özel üçgenlerinden birisidir 15 75 90 üçgeni kendine has kuralları olan bir üçgendir ve kuralları değişmez zaten değiştirildiği takdirde açı ve uzunluklarından ötürü özel üçgen olmaktan çıkar Bazı özel formül ve kurallar bizlere soru ve problem çözümünde oldukça fayda sağlar ve bizi




Index Of Wp Content Uploads 18 05




45 45 90 Ucgeni Matematikce
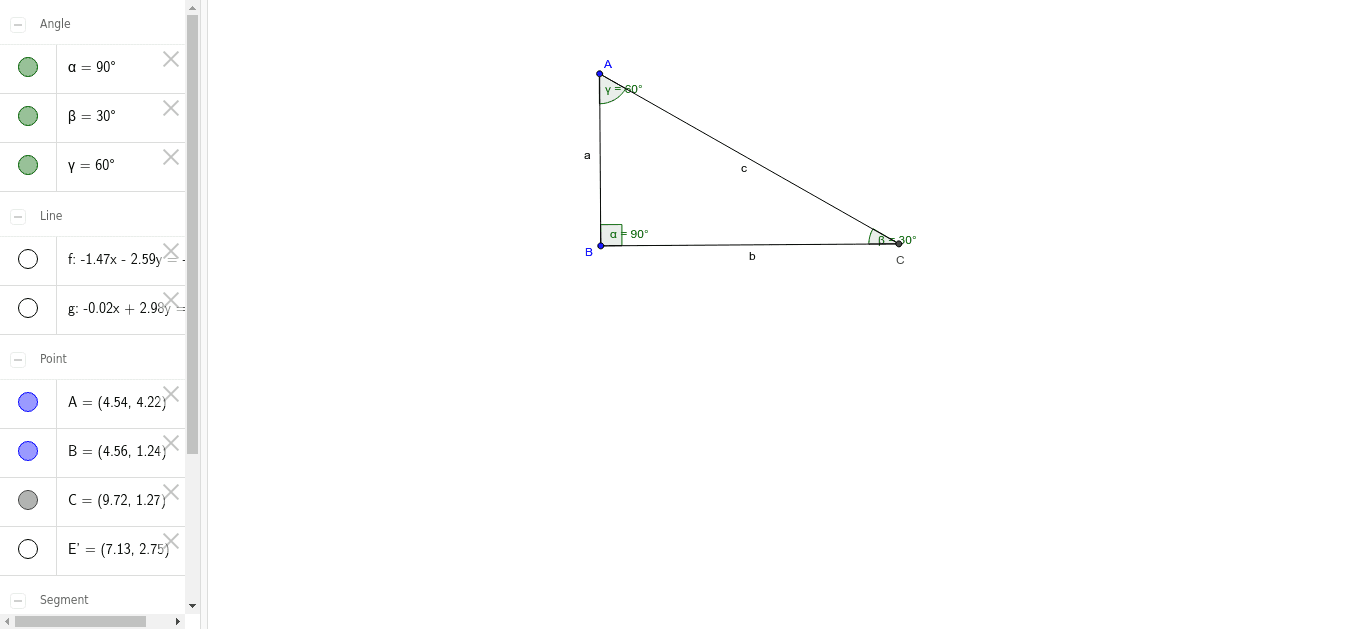
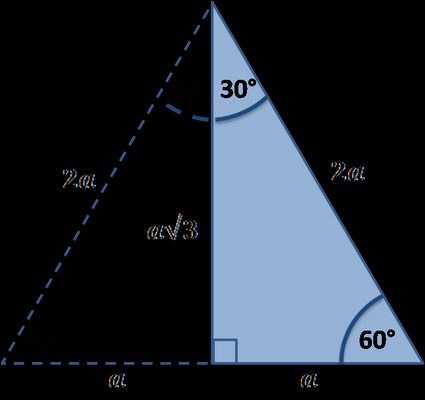
(30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° 60° 90°) üçgenleri elde edilir AB = AC = a BH = HC = pisagordan (30° 60° 90°) dik üçgeninde; Bu 30 60 90 üçgeni bir eş üçgenin yükseklik ile iki eş parçaya bölünmesinden oluşmuştur Bu üçgenin açıları 30 derece 60 derece ve 90 derecedir Bu açıları gören kenarların uzunluklarının ise belirli bir kuralı bulunmaktadır 30 derecelik açının gördüğü kenarın uzunluğu 90 derecelik kenarın gördüğü uzunluğun yarısı, 60 derecelik açının gördüğüVeya üçgeni gördüğünüzde bu orana göre, biraz önce gördüğümüz oranlara göre kenar uzunluklarını bulabilirsiniz Mesela kenarları 2, 2 kök 3 ve 4 olan bir üçgen gördünüz 2'nin 2 kök 3'e oranı, 1 bölü kök 3 2'nin 4'e oranı da 1 bölü 2'dir Dolayısıyla bu üçgen üçgenidir Bu videoda size, geometri ve trigonometride çok karşımıza çıkan
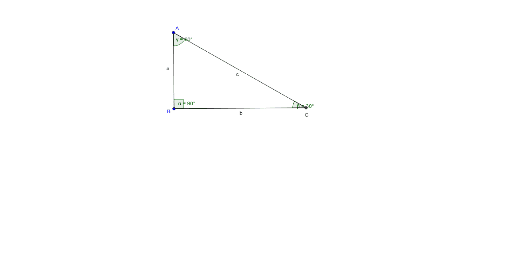



Triangle 30 60 90 Geogebra




Ucgenler Dik Ucgenler 4 30 60 90 Ucgeni Geometri Metin Hocam Youtube
üçgeni 90 60 30 üçgeni kpss konu anlatımı Özel Üçgenler Dik üçgen – İkizkenar Üçgen – Eşkenar Üçgen Henüz Yorum Yazılmamış ilk yorumu sen yap Bir Cevap Yazın Cevabı iptal et 0 Takip Et 743 Takip Et 2,996 Beğen Ara Eğitim Caps Bizi Takip Edin! 15 Derece Kuralı Kullanım Kılavuzları KALORİMETRE HAKKINDA BİLGİLER VE KULLANIMINDA DİKKAT EDİLECEK HUSUSLAR Kalorimetre takılı olan binalardaki faturalandırma sistemi şu şekildedir, binaya gelen faturanın % 30u dairelerin m*2 sine göre dağıtılırDik Üçgen, Pisagor Bağıntısı, Özel Dik Üçgenler, İkizkenar dik üçgen, (30° – 60° – 90°) Üçgeni, (30° – 30Art of Problem Solving's Richard Rusczyk discovers the relationships among the sides of a triangle




Amal Triangle For Android Apk Download




30 60 90 Ucgeni Ispat Youtube
30 60 90 üçgeni 30 60 90 üçgeni çoğu soruda karşımıza gelir o nedenle bu üçgenin özelliklerini iyi bilmek gerekir Olay çok basit öncelikle dik üçgeni tanıyalım Dik üçgen olması için zaten üçgenin açılarından biri 90 derece olmalı Önce bu 90 derecelik açıyı bulun bu açının karşısındaki kenara hipotenüs adı verilir ve bu kenar dik üçgenin en uzun √ 15 75 90 üçgeni kuralı 75 90 üçgenin kuralı Daha iyisi yapılana kadar en iyisi bu75 15 90 üçgeni özelliği;Mm lens sample photos;üçgeni ve ispatı Açıları olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır 30°'nin karşısındaki kenarın katıdır İspatı ise eşkenar üçgen vasıtasıyla yapılır Kenarları 2 cm olan bir eşkenar üçgende köşeden indirilen dikme kenarı iki eş




45 45 90 Ucgenleri Video Khan Academy




Special Right Triangles Sine Cosine Tangent Flashcards Quizlet
🌸Sorularınızı ve hangi konudan soru istediğinizi yorumlarda paylaşabilirsiniz 🌿🌸Videoyu beğendiyseniz beğen tuşuna basarak ve kanalıma abone olarak bana d Geometride karşımıza çıkan özel dik üçgenler bulunmaktadır Bu özel dik üçgenlerden bir tanesi ise 30 60 90 üçgenidir Bu 30 60 90 üçgeni bir eş üçgenin yükseklik ile iki eş parçaya bölünmesinden oluşmuştur Bu üçgenin açıları 30 derece 60 derece ve 90 derecedir Bu açıları gören kenarların uzunluklarının ise belirli bir kuralı bulunmaktadır 30 derecelikBuna geometri dersinde muhteşem üçlü denir ÜçgeniBir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısına eşittir Üçgeni60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittirÖklid Teoremi




30 60 90 Ucgeni Youtube



The Easy Guide To The 30 60 90 Triangle
45 45 90 Üçgeni, özel üçgenlerden biri olup, geometri dersinde çok önemli bir yeri bulunmaktadır Trigonometrik bağıntıları çok iyi idrak etmek için 45 45 90 üçgenini çok iyi bilmek gerekirBu nedenle, bu üçgeni çok iyi bilmek karşılaşılacak tüm30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5 (30° 30 30 60 90 üçgeni kuralı bir dik üçgen üzerinden ele alınan sabit bir üçgendir 30 derecenin karşısında olan kenar hipotenüs uzunluğunun yarısına verir 60 derecenin karşısında olan kenar ise, 30 derecenin gördüğü kenar üzerinden kök 3 ile çarpılır Aynı şekilde 90 derecenin karşısında olan kenar ise, 30 derecenin karşısındaki kenarının 2 katı olarak ifade




Ispat 30 60 90 Ucgeninde Kenarlarla Acilar Arasindaki Iliski Tyt Geometri Ozel Ucgenler Youtube




180 Geometry Ideas In 21 Teaching Math Math Geometry Education Math
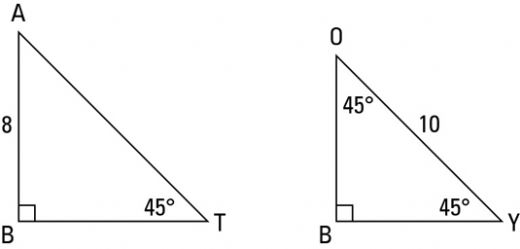
45 45 90 üçgeni de işimizi kolaylaştıracak özel üçgenlerden biridir 45 45 90 üçgenini iyi öğrenirsek temel bazı trigonometrik bağıntıları da öğrenmiş oluruz Bu nedenle bu üçgeni ve özelliklerini bilmek önemlidir Öncelikle en az bu üçgen kadar önemli 30 60 90 üçgeni olduğunu belirtelim Bu özel üçgenleGeometri dersinde bilmemiz gereken bazı özel üçgenler bulunmaktadır Bu özel üçgenler arasında 15 75 90 üçgeni de bulunmaktadır 15 75 90 üçgeni30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5 (30




180 Geometry Ideas In 21 Teaching Math Math Geometry Education Math




30 60 90 Triangle Calculator Formula Rules
üçgeni kenar uzunlukları bulma 30 derecenin karşısındaki kenarın uzunluğu hipotenüs uzunluğunun yarısına eşit olur60 derecenin karşısındaki kenarın uzunluğu ise hipotenüsün yarısı alınıp birde kök 3 ile çarpılarak bulunur Örnek üçgeni ( 30 60 90 üçgeni özel oranları olan önemli bir üçgendir Bu tür üçgenlere özel üçgenler denir Özel üçgenlerin özelliklerini bilmek geometri sorularını çözmek açısından çok önemlidir Çünkü bu üçgenler geometrinin neredeyse her konusunda karşımıza çıkar Bunun da ötesinde trigonometri konusu başta olmak üzere matematiğin birçok konusunda 30 60 90




30 60 90 Ucgeni Youtube
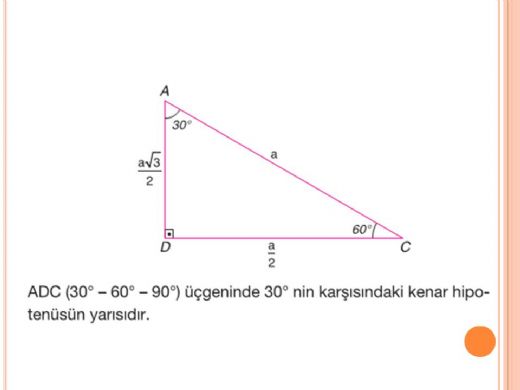



30 60 90 Ucgeni Pisagormatik



45 45 90 Ucgeni Matematikce
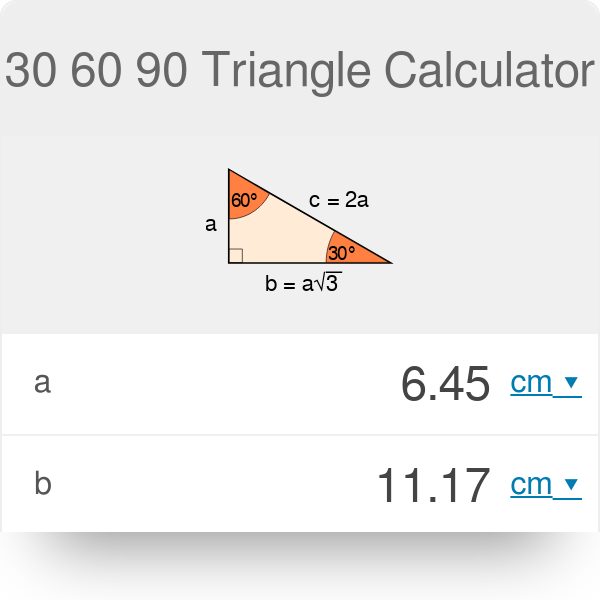



30 60 90 Triangle Calculator Formula Rules
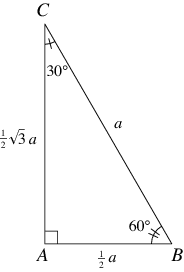



30 60 90 Triangle From Wolfram Mathworld




Problemas Matematicos Photos Facebook




Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim




30 60 90 Ucgeni Matematik Geometri Ve Turkce Blogu Dgs Ales Kpss



Is A 3 4 5 Triangle Also A 30 60 90 Triangle Quora



Angle And Trigonometric Functions 11 10 Sideway Output To




30 60 90 Ozel Ucgeninde 60 In Karsisi Tam Sayi Olursa 30 Ve 90 I Nasil Bulcaz Denklemi Yazabilen Eodev Com
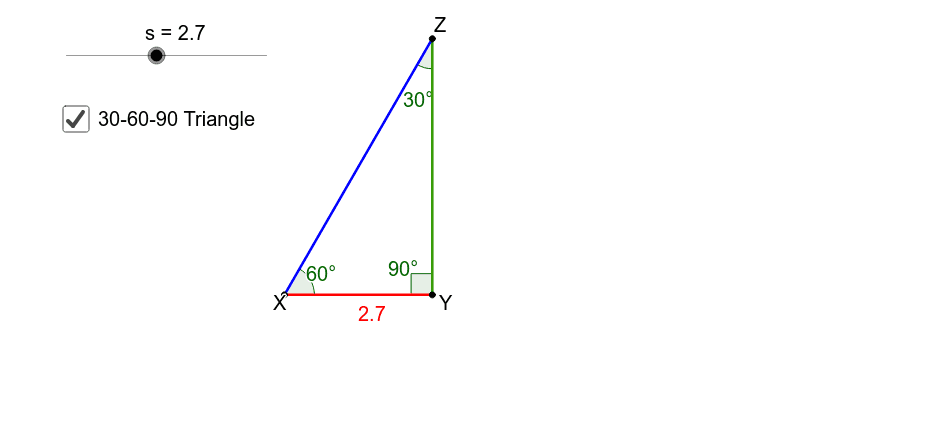



Special Right Triangles 30 60 90 Geogebra




Triangle Degrees Stock Illustrations 251 Triangle Degrees Stock Illustrations Vectors Clipart Dreamstime




Index Of Wp Content Uploads 18 05




En Hizli 30 60 90 Ucgeni




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




5 Soru 30 60 90 Ucgeni Youtube
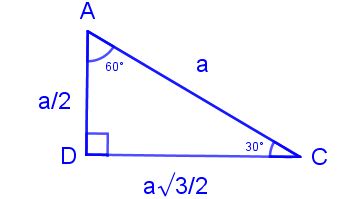



30 60 90 Ucgeni




Index Of Wp Content Uploads 17 10




High School Mathematics Lessons More Examples On 30 45 60 Degree Triangles




30 60 90 Ucgeni Ispat Youtube
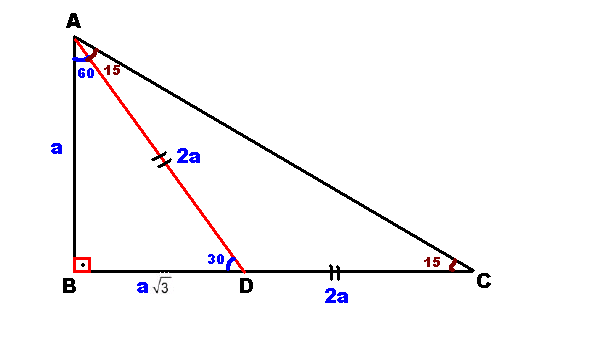



En Hizli Geometri 30 60 90 Ucgeni Ozellikleri




Finding A Tringle S Side Length Using A Cosine Function Practice Study Com




30 60 90 Triangle Calculator Formula Rules




How Do You Solve The Right Triangle Given The Hypotenuse Is 4 And



A 1 6m Tall Person Stands Right Beneath The Bulb Fitted At The Ceiling Of The Room And Therefore Makes No Shadow She Moves 2 Meters To Make The Length Of Her Shadow




30 30 1 Ucgeni Not Bu




90 60 30 Ucgeni



30 60 90 Triangle Calculator Formula Rules




Index Of Wp Content Uploads 17 10




Nereden Cikti Bu 30 60 90 Ucgeni 30 60 90 Ucgeni Ispati Youtube




Trigonometry



Onenushighlights Com



Axisobject Wolfram Language Documentation




30 60 90 Ucgeni Turleri Ve Ozellikleri




Dik Ucgen 14 30 60 90 Ucgeni Ayrik Matematik Evde Egitim Psikoloji




30 60 90 Ucgeni



45 45 90 Ucgeni Youtube



The 9 81 90 Triangle Robertlovespi Net




Cot 90 Kactir Iae News Site




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




30 60 90 Ucgeni Ve Ozellikleri Not Bu




30 60 90 Ucgeni Youtube



Triangle 30 60 90 Geogebra



Dik Ucgende Trigonometrik Oranlar



Triangle Degrees Stock Illustrations 251 Triangle Degrees Stock Illustrations Vectors Clipart Dreamstime



30 60 90 Ucgeni Kurali Nedir 30 60 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri



En Hizli 30 60 90 Ucgeni Kurali




70 90 Ucgeni Hd Png Download Transparent Png Image Pngitem



3




Dik Ucgen 30 60 90 Dik Ucgeni Youtube
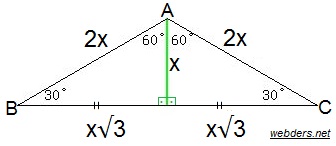



1 30 30 Ucgeni Webders Net




180 Geometry Ideas In 21 Teaching Math Math Geometry Education Math



30 60 90 Triangle Calculator Formula Rules
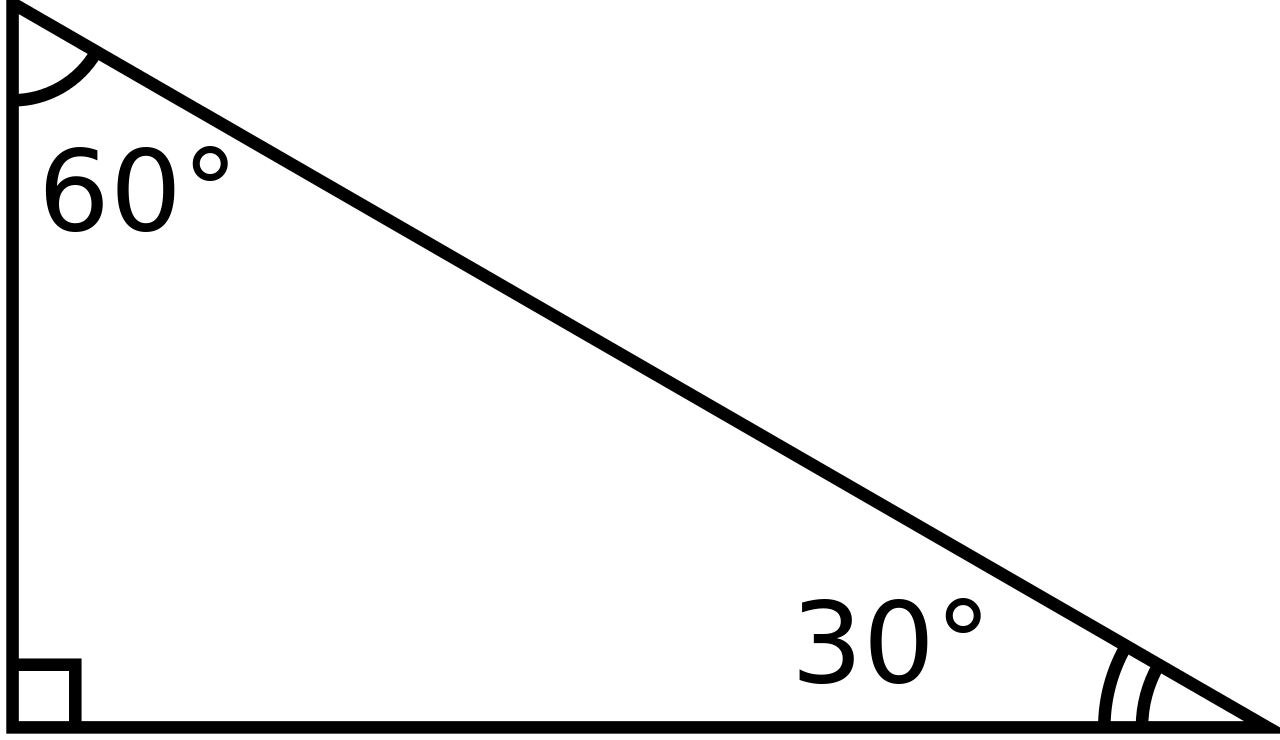



File 30 60 90 Triangle 2 Svg Wikimedia Commons
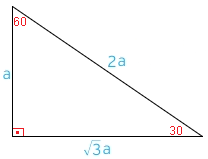



30 60 90 Ucgeni Webders Net



The Easy Guide To The 30 60 90 Triangle
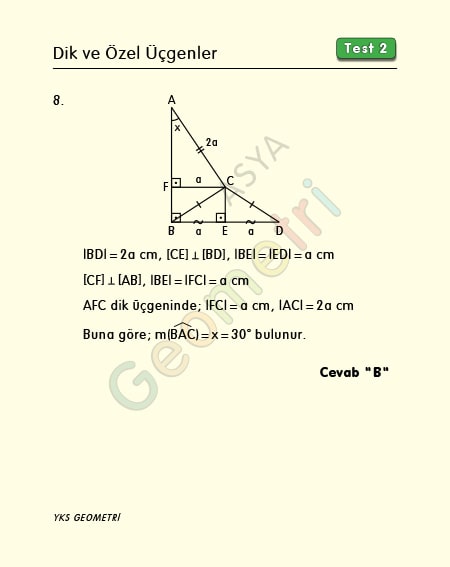



Vertical And Special Triangles Test 2 Course Geometry




En Hizli 30 60 90 Ucgeni Trigonometrik Oranlari



Teog Trigonometri Ozel Ucgenler Konu Anlatim Video Ozancorumlu Com Turkiye Nin Egitim Sitesi



Oklid




45 45 90 Ucgeni Ve Ozellikleri Not Bu
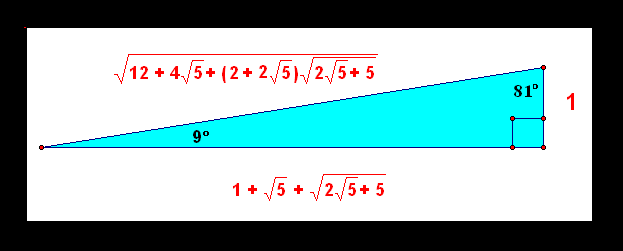



The 9 81 90 Triangle Robertlovespi Net



The 27 63 90 Triangle Robertlovespi Net
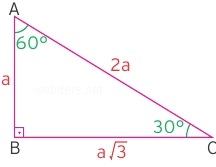



En Hizli 30 60 90 Ucgen Kenarlari



Jagpal Weebly Com




30 60 90 Ucgeni Ibrahim Hocca




Dik Ucgende 30 Un Karsisi 3 Ise 60 Ve 90 In Karsisi Ne Olur Eodev Com



90 60 30 Ucgeni




Gmtri




30 60 90 Ucgeni Akilli Geometri



1



Dik Ve Ozel Ucgenler 1



45 45 90 Ucgeni Turleri Ve Ozellikleri



0 件のコメント:
コメントを投稿